Ця стаття висвітлює важливі аспекти процесу складання розкладу для вищих навчальних закладів, математичні методи та алгоритми, які допомагають у процесі складання розкладу, детально розглянутий генетичний алгоритм для вирішення цієї проблеми, а також на його основі побудовано власний метод складання розкладу

КЛЮЧОВІ СЛОВА: математичне моделювання, розклад, складання розкладу, університет, еволюційні методи, генетичний алгоритм, фітнес-функція,схрещування, мутація

АКТУАЛЬНІСТЬ. Складання розкладу являє собою надзвичайно трудомісткий та складний процес, який полягає у встановленні послідовності зустрічей викладачів і студентів у заздалегідь заданий проміжок часу (як правило, протягом тижня), з урахуванням задоволення низки обмежень різного характеру. Беручи до уваги  той факт, що в більшості українських ВНЗ складання розкладу відбувається вручну, при цьому, в зв’язку з надзвичайною складністю урахування всіх обмежень, велику увагу приділяють автоматизації складання розкладу. Проте процесу автоматизації передує розробка правильного математичного алгоритму, на основі якого створюватиметься система. Він являється ядром всієї системи, тому перш ніж сідати за проектування та розробку програмного продукту, потрібно скласти правильну математичну модель та метод (алгоритм) для системи. Це є надзвичайно складним процесом, оскільки потрібно враховувати безліч чинників та факторів, таких як навантаження студентів, навантаження викладачів, аудиторний фонд ВНЗ, поділ груп на підгрупи, необхідність спеціалізованих приміщень для проведення лабораторних занять та  багато інших. Актуальність цієї теми полягає в тому, що не зважаючи на те, що є велика кількість методів та алгоритмів для задачі складання розкладів, ще не існує універсального алгоритму, який би здійснював складання розкладу для вищих навчальних закладів без втручання людини. 

АНАЛІЗ ДОСЛІДЖЕНЬ І ПУБЛІКАЦІЙ. Дослідженням даної теми займалися і продовжують займатись науковці із всього світу, втому числи із України.

Бойко О.М. з черкаського державного технологічного університету обґрунтував необхідність створення автоматизованої системи складання розкладу занять. Для цього автор пропонує використовувати генетичний алгоритм. Най його основі формує цільову функцію, необхідні обмеження, формує початкову популяцію та показує приклади, як проводяться такі операція як кросове та мутація. Використовуючи ці знання, автором була побудова система на базі об’єктно-орієнтовних принципів, яка перевіряла залежність час виконання генетичного алгоритму від розміру задачі. Бойко О.М. дійшов висновку, із збільшенням розмірності, збільшується час розв’язання задачі. Також було зазначено, що розв’язок отриманий за допомогою такого алгоритму близький до оптимальності але не оптимальний [2].

С. В. Бевз, В. В. Войтко, С. М. Бурбело, А. М. Шоботенко займались розробкою автоматизованої системи формування розкладу магістратури Вінницького національного технічного університету. Автори створили математичний алгоритм на основі якого повинна працювати система. Сама ж безпосередньо здійснена засобами об’єктно-орієнтовної мови програмування PHP [1].

Цзянь Ні (Jian Ni) з Хебейського університету інженерії (Китай) у своїй праці обґрунтував необхідність створення автоматичної системи створення розкладу. Так наприклад, з 1999 року в Китаї була введена нова політика, щодо зарахування в університет. Внаслідок цього значно зросла кількість студентів, а через це в свою чергу значно ускладнилась робота навчально-методичних відділів. Для вирішення проблеми автор пропонує використовувати генетичний алгоритм, як ефективний метод для розв’язку[10].

Кулдіп Кумар (Kuldeep Kumar), Рамеш Шарма (Ramesh Sharma), Каушал Мехта (Kaushal Mehta) із університету імені Чаудхари Деві Лал (Сирса, Індія) у своїй роботі використовували генетичний алгоритм. Авторами було визначені жорсткі та м’які обмеження, було наведено схему генетичного алгоритму, показані приклади схрещування та мутації, сформована фітнес-функція та початкова популяція. Для практичної реалізації свого алгоритму, використовувалась бібліотека мови програмування C++ для генетичних алгоритмів GALIB 247. В результаті  практичної верифікації було виявлю, що із збільшенням популяції, порушення м’яких та жорстких обмежень зменшуються[11].

ОСНОВНА ЧАСТИНА

1. Генетичний алгоритм

На сьогоднішній день існує багато методів та алгоритмів для вирішення задачі складання розкладу в університеті. Так, модель задачі складання розкладу в рамках лінійного цілочисельного програмування містить ряд недоліків, пов’язаних як з неповною адекватністю представленого розв’язку задачі, так і значною трудомісткістю використання запропонованого комплексу програм, що вимагає участі кваліфікованого користувача. Метод імітації випалювання та алгоритм розфарбовування графу, незважаючи на зовнішню простоту, можуть виявитися цілком ефективними для складання лише невеликих розкладів. При реалізації алгоритму, що базується на принципах імітаційного моделювання, обмежується можливість застосування розробленої системи в інших ВНЗ, крім того, знадобиться вносити істотні зміни в алгоритм при незначних внутрішніх змінах у ВНЗ [2].

Багато дослідників як сьогодні так і в минулому приклали багато зусиль для того, щоб розробити універсальну автоматизовану систему для складання розкладів. Проте ще до сьогодні немає досконалого рішення в цьому питанні. Можливим рішенням цієї проблеми може бути використання генетичних алгоритмів.

Генетичний алгоритм (англ. genetic algorithm) — це еволюційний алгоритм пошуку, що використовується для вирішення задач оптимізації і моделювання, шляхом послідовного підбору, комбінування і варіації шуканих параметрів з використанням механізмів, що нагадують біологічну еволюцію.

Цей метод заснований на аналогії з природними еволюційними процесами. Його перевагою є те, що не висуваються додаткові вимог до виду цільової функції, на кожній ітерації працює з множиною рішень, що дозволяє в багатьох випадках більш детально в порівнянні з градієнтними методами багатовимірної нелінійної безумовної оптимізації аналізувати простір пошуку [7].

Особливістю генетичного алгоритму є акцент на використання оператора “схрещення”, який виконує операцію рекомбінацію рішень-кандидатів, роль якої аналогічна ролі схрещення в живій природі.

«Батьком-засновником» генетичних алгоритмів вважається Джон Голланд (англ. John Holland), книга якого “Адаптація в природних і штучних системах” (англ. Adaptation in Natural and Artificial Systems) є фундаментальною в цій сфері досліджень.

Згідно з еволюційною теорією Чарльза Дарвіна біологічні світи, для того щоб вижити, повинні пристосовуватися до навколишнього середовища і разом з тим відбувається біологічна спадкоємність нащадками життєво важливих властивостей від батьків. Відповідно до експерименту Освальда Евері, Коліна Маклауда  і Макліна Маккарті зробленого в 1944 році, та на основі сучасних досліджень із цитології та генетики, матеріальною основою спадковості і мінливості організмів  є хромосомна ДНК – основний генетичний матеріал.

При моделюванні цим методом, активно використовується понятійний апарат генетики. Тому слід доти визначення наступним поняттям:

– ген – реально існуюча, незалежна одиниця спадковості, що комбінується й розщеплюється при схрещуваннях;

– хромосома – структурний елемент клітинного ядра біологічних організмів, є носієм генів у клітинному ядрі особини. У генетичних методах терміни «хромосома» та «особина» використовуються як синоніми;

– популяція – досить велике співтовариство організмів, що схрещуються між собою. Популяції характеризуються набором ланцюжків генів кожного з об’єктів, сукупність яких визначає генофонд популяції [7].

Генетичний алгоритм має такі переваги:

– відсутність необхідності в специфічних знаннях про вирішувану задачу. Проте у випадку, якщо додаткова інформація про досліджувану систему, об’єкт або процес є відомою, то вона може бути використана в процесі пошуку;

– концептуальна простота та прозорість реалізації;

– можливість розпаралелювання;

– простота кодування вхідної і вихідної інформації. Некритичність до виду параметрів досліджуваних систем (можливість використання експертної, емпіричної, довідкової та іншої інформації про об’єкт, поданої різними типами даних);

– можливість застосування до великого кола задач без внесення серйозних змін у внутрішню структуру методу;

– можливість адаптивності параметрів генетичного пошуку до особливостей вирішуваної задачі;

– менша ймовірність попадання і зациклення в локальному оптимумі, яка досягається за рахунок використання популяційного підходу;

– можливість застосування в методі інших пошукових процедур [7].

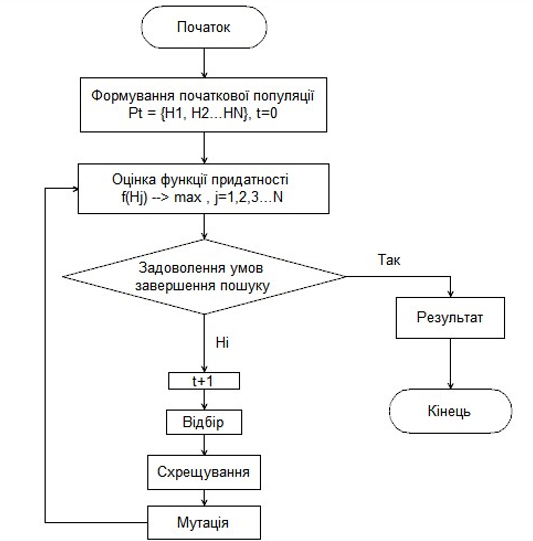
Генетичний алгоритм реалізується у декілька етапів (рис. 1) :

Рис. 1. Схема роботи генетичного алгоритму

2. Обмеження

Проблема процесу складання розкладу полягає і втому, що розклад повинен відповідати ряду обмежень. Усі обмеження поділяють на так звані м’які та жорсткі.

Жорсткі – це обмеження, які повинні неодмінно задовольнятися; такі які фізично не можуть бути порушені (наприклад один і той самий викладач не може бути присутній в один і той самий час у двох місцях одночасно).

М’які – це обмеження, які можна порушувати, але це порушення повинно бути зведене до мінімуму. Їхнє виконання не є таким же обов’язковим, як жорстких. У таблиці 1 наведені жорсткі та м’які обмеження які необхідні для процесу складання розкладу:

Таблиця 1

Обмеження для процесу складання розкладу

Жорсткі

М’які

викладач   не може бути присутнім на двох заняттях одночасно;   в одній аудиторії не можуть проводитися різні   заняття одночасно;   місткість аудиторії не може бути меншою, ніж   кількість присутніх у ній студентів;   деякі заняття вимагають особливих аудиторій   (наприклад комп’ютерних класів, лабораторій, спортзалів та інше ); одна група не може вивчати декілька   дисциплін на одному занятті одночасно; тижневе навантаження для студентів   бакалаврату становить 30 годин; тижневе навантаження для   студентів-спеціалістів 24 годин; тижневе навантаження для   студентів-магістрів становить 18 годин;  кількість   занять на день не більше 4

викладачі можуть віддавати перевагу конкретним   часовим інтервалам;   викладачі можуть віддавати перевагу певним   аудиторіям;   деякі види предметів не повинно бути в суміжні   в часові;   уникнення проміжних періодів в розкладі (вікна);   рівномірний розподіл занять протягом тижня;   місткість аудиторій не повинна бути набагато   більшою ніж кількість присутніх студентів; більш складні заняття потрібно проводити   на 1-2 парі; фізичне виховання рекомендується проводити   3-4 парою;

3. Вхідна інформація

Хромосома – це набір генів. У нашому випадку цим набором являються заняття в розкладі. Хромосоми представляють у вигляді масиву даних, кожний елемент якого – це одне заняття в розкладі. Для того, що створити хромосому будемо використовувати таку вхідну інформацію:

1) T = {t_w, t_d, t_p} – множина часу проведення робочих занять (пар), де  {1…N_w}- номер тижня,  = {1…N_d}- номер дня тижня,  = N_p}- номер пари протягом дня;

2) G = { g₁, g₂…g_Ng } – множина груп в університеті, де g_i – номер навчальної групи, N_g – загальна кількість навчальних груп;

3) L = { l₁, l₂…l_Nl } – множина викладачів університету, де l_i– номер викладача, N_lзагальна кількість викладачів в ;

4) D = { d₁, d₂…d_Nd } – множина дисциплін, де D_i– номер навчальної дисципліни, N_d– загальна кількість дисциплін в університеті;

5) A = { a₁, a₂…a_Na} – множина аудиторій університету, де a_i– номер аудиторії, N_a– загальна кількість аудиторій в університеті [3;7].

Треба відзначити, що такий поділ не являється достатньо деталізованим, оскільки, наприклад,  не враховуються тип аудиторій. Тому потрібно детальніше поділити ці множини.

3.1 Аудиторії

Проведемо поділ аудиторій на три типи:

1)      аудиторії для проведення лекційних занять (потокові) – A_b;

2)      аудиторії для практичних занять (для однієї групи/підгрупи) – A_s;

3)      лабораторні аудиторії (комп’ютерні класи, спец аудиторії та інше) – A_l.

Таким чином : A=A_b U A_s U A_l ,   тип аудиторії і приймає значення b, s, l.

3.2 Взаємозв’язок множин дисципліна, викладач та група

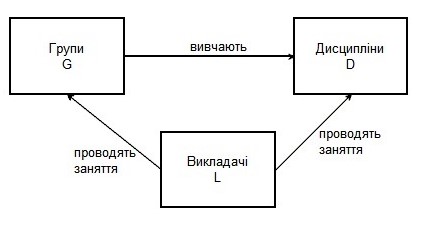
Між такими множинами як дисципліна, викладач та група існує тісний зв’язок, оскільки групи вивчають певні дисципліни, які проводяться конкретними викладачами (рис.2).

Рис. 2. Взаємозв’язок множин «Групи», «Дисципліни» та «Викладачі»

Як наслідок утворюється нова множина, яку назвемо «Знання» і можемо представити наступним чином:

Z = {z_i} = , де  викладач;  дисципліна;  група;  тип занять;  необхідна аудиторія.

3.3 Кодування інформації

Для того щоб створити певну особу (хромосому), яка в нашому випадку є одним заняттям у розкладі, потрібно правильно закодувати вхідну інформацію. Для цього можна використовувати три методи:

1)      бінарне кодування – гени у хромосомах можуть приймати значення 0 або 1;

2)      числове – гени можуть приймати значення в заданому інтервалі;

3)      векторне – гени є вектором цілих чисел [7].

На нашу думку найкращим методом для кодування такого роду інформації є числовий. Хоч і в класичному генетичному алгоритмі зазвичай кодування відбувається бінарним способом, але для цієї задачі такий метод має ряд недоліків, які впливають на швидкість та збіжність алгоритму. До прикладу, числа 7 та 8 у десятковому представленні відрізняються однією позицією, а от у бітовому (0111 та 1000) – чотирма [2]. Недоліком векторного кодування є те, що вектор не може містити однакових чисел.

Розгляньмо приклад, де початковими даними для складання розкладу є 2 тижні, 5днів тижня, 5 пар на день; 30 викладачів, 70 дисциплін, 20 навчальних груп, 100 аудиторій.

Отже, кодування хромосоми буде наступним: на кодування множини робочих занять відводиться 3 знаки (тижні, дні тижня, пар в день [1,2; 1…5; 1…5] ), на кодування множини знання 10 знаків (викладачі, тип заняття, дисципліни, навчальні групи, аудиторія – [1…30; 1…3; 1…70; 1…20; 1…100] ). Таким чином хромосома містить у собі 13 знаків, а популяція міститиме 1000 особин ( 2тижні*5днів*5пар*20груп). Наприклад одна з особин буде виглядати так:

1 2 3 27 2 54 14 098

і означатиме, що на першому тижні (1), у вівторок (2) на третій парі (3), викладач під номером 27 вестиме практичне (2) заняття з дисципліни під номером 54 в 14 групі у 98 аудиторії.

4. Цільова функція (фітнес-функція)

Рішення щодо хромосоми (особини) оцінюється за допомогою значення цільової функції, тобто перевіряється, чи придатна особина для подальшого використання. Цільову функцію часто називають фітнес-функцією чи функцією придатності. Значення цієї функції оцінюється для кожної хромосоми популяції окремо і на його основі, приймається рішення використовувати цю хромосому чи перейти до етапу покращення особин популяції, за допомогою генетичних операторів схрещування та мутації. Для нашої задачі нами було розроблена наступну цільову функцію:

де H_j – оцінювана хромосома;

 – ваговий коефіцієнт викладача p, щодо проведення занять у t_d  день тижня;

t_d  = {1…N_d}- номер дня тижня, N_d – кількість робочих днів у тижні;

v_g – ваговий коефіцієнт, щодо наявності у t_d  день тижня проміжних періодів у розкладі («вікон») для g групи;

 – кількість вікон у день t_d  (якщо вікон немає то  = 1);

Q – бінарна змінна, яка побудована на основі жорстких обмежень і визначається наступним чином:

де  = {1…N_w}- номер тижня;

 = {1…N_d}- номер дня тижня;

 = {1…N_p}- номер пари протягом дня.

Якщо цільова функція = 0, то це означає, що не виконалось якесь із жорстких обмежень, тому досліджувана хромосома є непридатною і підлягає покращенню своїх характеристик.

Цільова функція застосовується щодо кожної особини (хромосоми) популяції і спрямована на знаходження максимального значення.

5. Генетичні оператори

Як ми вже раніше зазначали, після того як сформуємо початкову популяцію, переходять до етапу оцінки кожної особини. Ті хромосоми, які задовольняють умови завершення пошуку відбираються із поточної популяції і будуть надалі використовуватися. Ті які ж не відповідають вимогам – піддаються покращенню за допомогою генетичних операторів, таких як схрещування або кроссовер та мутація.

Ці операції призначені для покращення поточної популяції та формування нової, особи якої краще пристосовані. 

5.1 Схрещування

Схрещування – це один із видів оператора рекомбінації генетичного алгоритму. В науковій літературі зустрічається ще під назвою кроссовер чи кросинговер.

Метою оператора схрещування є породження з наявної множини рішень нового, в якому кожна хромосома буде нащадком деяких двох елементів попередньої популяції, тобто нести в собі частково інформацію кожного батька. Допускається ситуація, коли обидва батька подані одним і тим же елементом популяції [7].

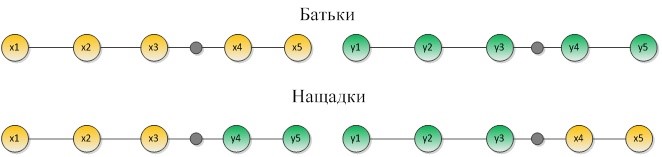
Найпростіший метод кроссоверу проводиться наступним чином: розмноження в генетичних алгоритмах зазвичай статеве – щоб «народити» нащадка, необхідно декілька батьків, зазвичай потрібна участь двох. Тому із поточної популяції вибирають або випадковим чином, або найбільш пристосовані дві особини. Далі випадковим чином всередині хромосом визначається точка розриву. Ця точка ділить хромосоми на дві частини, якими потім обмінюються. Таким чином ми получаємо нащадків, які успадкували певні характеристика від батьків. Процедура проведення цієї операції зображена на рисунку 3.

Рис. 3. процедура проведення одноточкового кроссоверу

Але на нашу думку цей генетичний оператор не підходить для проблеми складання розкладу, оскільки може значно спотворити наші вхідні дані.

Розглянемо простий приклад. Нам потрібно провести операцію схрещування. Для цього ми відібрали дві особини:

Х: 7 3 1 27 2 54 15 38

У: 9 2 4 68 1 63 3 27

Тепер визначимо точку розриву:

Х: 7 3 1 27 2 . 54 15 38

У: 9 2 4 68 1. 63 3 27

Проведемо обмін частинами та утворимо нащадків:

Х₂: 7 3 1 27 2 63 3 27

У₂: 9 2 4 68 1 54 15 38

Із проведеної операції бачимо, що із батьківських хромосом X і Y утворилися два нащадки Х₂ та У₂. Проте слід звернути увагу на те, що в першому випадку хромосома Х означала проведення 27 викладачем 54 предмету у групі  під номером 15. А після схрещування, що 27 викладач проводить заняття з дисципліни 63 у групі 3. Це означає, що викладач повинен викладати зовсім інший предмет для іншої групи. Тобто на практиці це те саме, що заставити викладача правничого факультету викладати економетричний аналіз для групи економічного факультету. Звичайно ж така ситуація в реальних умовах не допускається. Тому для завдань складання розкладу за допомогою генетичного алгоритму ми не рекомендуємо застосовувати операцію схрещування.

5.2 Мутація

Оператор мутації полягає в зміні генів у випадково вибраних позиціях. На відміну від оператора схрещування, які використовуються для поліпшення структури хромосом, метою оператора мутації є диверсифікація, тобто підвищення різноманітності пошуку і введення нових хромосом в популяцію для того, щоб більш повно досліджувати простір пошуку. Мутація ініціює різноманітність в популяції, дозволяючи проглядати більше точок в просторі пошуку і долати таким чином локальні екстремуми в ході пошуку [7].

Необхідно відзначити, що оператор мутації є основним пошуковим оператором і існують методи, що не використовують інших операторів окрім мутації.

Для вирішення нашої задачі будемо використовувати просту мутацію, яка використовується для бінарних, гомологічних, числових і векторних хромосом.

Алгоритм здійснення операції складається з таких кроків:

1. Скопіювати батьківську хромосому в хромосому-нащадка;
2. Вибираємо випадковим чином ген для мутації;
3. У заданому інтервалі допустимих значень гена вибрати нове значення, що не дорівнює поточному.

Наприклад маємо хромосому Х: {7 3 1 27 2 63 3 27} і хочемо застосувати до неї операцію мутації. Будемо виконувати процедуру поетапно:

1)      Копіюємо батьківську хромосому в хромосому-нащадка:

Х: {7 3 1 27 2 63 3 27}  Х₂: {7 3 1 27 2 63 3 27}

1)      Вибираємо випадковим чином ген для мутації:

Х₂: {7 3 1 27 2 63 3 27}

2)      У заданому інтервалі допустимих значень гена вибираємо нове значення, що не дорівнює поточному:

Х₂: {7 1 1 27 2 63 3 27}

Після того як провели операцію хромосому нащадка слід оцінити за допомогою фітнес-функції. Якщо значення фітнес функції покращилося, то це означає що операція мутації успішно покращила характеристики хромосоми. Якщо ні, то слід проводити операцію допоки не отримаємо бажаного результату.

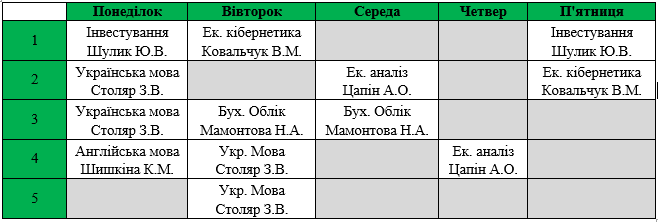
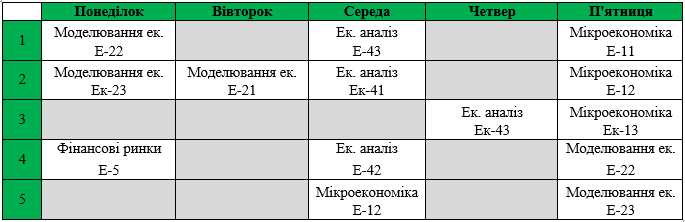
Для кращого сприйняття здійснимо операцію мутації на реальному прикладі. Припустимо ми маємо попередній зразок розкладу для групи Ек-43, який виглядає наступним чином:

Таблиця 2

Розклад навчальних занять для групи Ек-43на 1 – 5 вересня 2013 року

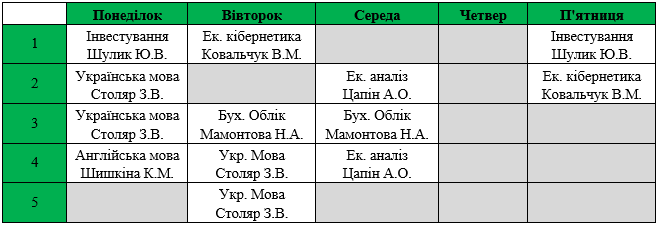
Також маємо індивідуальний розклад викладача Цапіна А.О. для цього ж тижня:

Таблиця 3

Індивідуальний розклад занять викладача Цапіна А.О. на 1-5 вересня 2013року

Проведемо операцію мутації для того, щоб покращити поточні результати. Для цього із популяції потрібно відібрати хромосому. Хромосоми складаються на основі таблиці 2 і виглядають наступним чином:

Таблиця 4

Розклад навчальних занять для групи Ек-43на 1 – 5 вересня 2013 року представлений у вигляді хромосом

Нами було вибрано для дослідження хромосому Х₁: 1 4 4 6 2 6 43 15.

Тепер потрібно вибрати ген для мутації. Ми вибрали 2-й порядковий ген, який відповідає за день тижня. Відповідно до алгоритму ми будемо міняти його значення на ті, які не дорівнюють його поточному значенню і одночасно будемо оцінювати особину за допомогою цільової функції. Заданий інтервал для цього гена {1, 2, 3, 4, 5}, що відповідає номеру дня тижня.

Для оцінки фітнес-функції нам потрібно задати вагові коефіцієнти для викладача, щодо проведення занять у певні дні тижня та вагові коефіцієнти, щодо наявності в розкладі проміжних періодів («вікон») .

Припустимо, що Цапін А. О. сформував вагові коефіцієнти наступним чином:  = {Пн.-0,15; Вт.-0,1; Ср.-0,3; Чт.-0,2; Пт.-0,25};

вагові коефіцієнти, щодо наявності проміжних періодів для групи Ек-43:

v₄₃ = {0,3-присутні проміжні періоди; 0,7-відсутні}.

Перш ніж приступати до процесу мутації давайте оцінимо поточне значення цільової функції для того, щоб порівнювати його із значенням, яке отримаємо після процесу мутації.

Оцінюємо цільову функцію:

 

Отож, проводимо мутацію:

X₂:  1 5 4 6 2 6 43 15

Як бачимо фітнес-функція = 0 і це означає, що хромосома Х₁ не придатна для використання, тому вона потребує повторного покращення через операцію мутації. Тому виконує процедуру до тих пір, допоки не отримаємо необхідне значення цільової функції.

X₃:  1 1 4 6 2 6 43 15

X₄:  1 2 4 6 2 6 43 15

X₅:  1 3 4 6 2 6 43 15

Бачимо, що після проведення останньої мутації наша цільова функція зросла, що свідчить про те, що ми покращили характеристики хромосоми і її можна використовувати в подальшому.

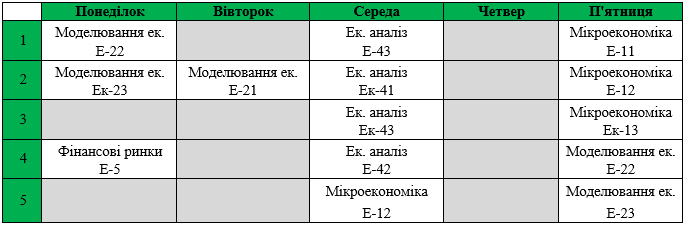
Тепер внесемо корективи у розклад занять і зробимо висновок, як змінилися наші дані. Отож розклад для групи тепер виглядає наступним чином:

Таблиця 5

Розклад навчальних занять для групи Ек-43 на 1 – 5 вересня 2013 року після проведення операції мутації

Індивідуальний розклад занять для викладача Цапіна А.О. після операції мутації наведено у таблиці 6.

Таблиця 6

Індивідуальний розклад занять викладача Цапіна А.О. на 1-5 вересня 2013року після проведення операції мутації

Порівнявши таблиці, можемо дійти висновку, що процес мутації покращив розклад занять як для викладача так і для групи. Оскільки замість того, щоб проводити одну пару в четвер, група з викладачем проведе її у середу. Разом з цим для групи появиться один день самоосвіти, а для викладача – вихідний день.

Отже можемо сказати, що процес мутацій і справді відіграє важливу для оптимізації поставленої перед нами задачі, за допомогою диверсифікації, тобто внесення змін в популяцію через зміну генотипу хромосоми.

ВИСНОВКИ

Процес складання розкладу це надзвичайно складний процес, який потребує від осіб які ним займаються неабияких вмінь та навичок. Його математично можна формалізувати, як складну оптимізаційну задачу для вирішення якої сьогодні існує ряд методів.

Ми детально розглянули еволюційний метод розв’язання оптимізаційної задачі, а саме генетичний алгоритм і можемо сказати, що  цей алгоритм заснований на аналогії з природними еволюційними процесами. Його перевагою є те, що не висуваються додаткові вимог до виду цільової функції, на кожній ітерації працює з множиною рішень, що дозволяє в багатьох випадках більш детально в порівнянні з градієнтними методами багатовимірної нелінійної безумовної оптимізації аналізувати простір пошуку.

Дослідивши, як застосовується генетичний алгоритм для проблеми складання розкладу в університетах,  можемо сказати, що цей метод має ряд переваг у порівнянні із іншими так як відсутність необхідності в специфічних знаннях про вирішувану задачу, концептуальна простота та прозорість реалізації, можливість розпаралелювання, простота кодування вхідної і вихідної інформації, можливість застосування до великого кола задач без внесення серйозних змін у внутрішню структуру методу та інші.

Під час виконання роботи було розроблено власний математичний метод для складання розкладу, а саме було визначено ряд обмежень, що враховуються при складанні розкладу, створено цільову функцію для оцінки придатності хромосом, вибрано генетичний оператор мутації, як головний інструмент покращення популяції шляхом диверсифікації, тобто внесення змін в генотип хромосом.

Загалом, генетичний алгоритм являється потужним інструментом для вирішення складних оптимізаційних задач і його практичне застосування сьогодні все частіше і частіше відбувається. 

ЛІТЕРАТУРА

1. Бевз С. В., Войтко В. В., Бурбело С. М., Шоботенко А. М. Розробка автоматизованої системи формування розкладу магістратури // Наукові праці ВНТУ. – Вінниця. – 2009. – Вип.1. – С. 1-10.
2. Бойко О.М. Еволюційна технологія розв’язування задачі складання розкладів навчальних занять // Штучний інтелект. – 2006. – Вип.3. – С. 341-348.
3. Кабальнов Ю.С., Шехтман Л.И., Низамова Г.Ф., Земченкова Н.А. Композиционный генетический алгоритм составления расписания учебних занятий // Вестник УГАТУ. Научные статьи и доклады: Информационные технологии – Уфа. – 2006. – №2(15). – С. 99-107
4. Ризун Н.О. Применение методов декомпозиции при решении многокритериальной задачи автоматизации составления расписания учебных занятий в ВУЗе // Восточно-Европейский журнал передовых технологий: Математика и кибернетика – фундаментальные и прикладные аспекты. – 2010. – №2/4(44). – С. 59-69.
5. Рутковская Д., Пилиньский М., Рутковская Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И.Д. Рудинского. – М.: Горячая линия-Телеком, 2006. – 452 с.
6. Сидорин А.Б., Ликучева Л.В., Дворянкин Методы автоматизации составления расписания занятий Часть 2. Эвристические методы оптимизации // Известия ВолгГТУ. – Волгоград. – 2009. – №12(60). – С. 120-123.
7. Субботін С.О., Олійник А.О., Олійник О.О. Неітеративні, еволюційні та мультиагентні методи синтезу нечіткологічних і нейромережних моделей: Монографія // Під заг. ред. С. О. Субботіна. – Запоріжжя: ЗНТУ, 2009. – 375 с.
8. Egwali A.O., Imouokhome F.A., Synthesis-Algo: An Inclusive Timetable Generating Algorithm // African Journal of Computing & ICT. – 2012. – Vol.5 No.4. – pp. 92-100.
9. Ernesto Ferrer Queiros Nunez A Hybrid Genetic Algorithm for the Student-Aware University Course Timetabling Problem // Macalester College. – 2010. – pp. 82.
10.  Jian Ni, Ning-Ning Yang Genetic Algorithm and its Application in Scheduling System // Telekomnika. – 2013. – Vol. 11 No.14. – pp.1934-1939.
11. Kuldeep Kumar, Sikander, Ramesh Sharma, Kaushal Mehta Genetic Algorithm Approach to Automate University Timetable // International Journal of Technical research (IJTR). – 2012. – Vol.1 Issue 1. – pp. 33-37.
12. Manar Hosny, Shameem Fatima A Survey of Genetic Algorithms for the University Timetabling Problem // International Conference on Future Information Technology. – Singpore. – 2011. – Vol. 13. – pp. 34-39.
13. Odim O.M., Oguntunde B.O., Alli O.O. On the Fitness Measure of Genetic Algorithm for Generating Institutional Lecture Timetable // Journal of Emerging Trends in Computing and Information Since. – 2013. – Vol. 4 No. 4. – pp. 436-444.0